Ruby TIPS
集合演算を行うには？
Rubyで配列を使って集合演算を行う方法として、「＆」演算子による積集合／「|」演算子による和集合／「-」演算子による差集合を説明する。
Rubyの配列を利用すれば、和集合や積集合といった集合演算が簡単にできる。数学的な演算にとどまらず、実用的にも便利な機能なので、具体例を見ながら紹介しよう。
集合演算はどのように使われているか
集合演算については、中学や高校の数学でも学ぶが、どのような場面で使われているか、あまり実感が湧かなかったかもしれない。現在では、集合演算はデータベースやWebページの検索などに利用されている。例えば、複数のキーワードの両方を含むWebページの一覧は積集合を求めていることになり、複数のキーワードのいずれかを含むWebページの一覧は和集合を求めていることになる。
ここでは、簡単な例を使って、積集合、和集合、差集合を求める方法を見てみよう。
積集合、和集合、差集合を求める
積集合とは、複数の集合の全てに含まれる要素の集合である。配列の&演算子を使うと積集合が求められる。
また、|演算子で和集合が求められる。
さらに-演算子で差集合が求められる。
まとめて見てみよう。
|
a = ["伊倉","高井","高城","玉井","百田","和川"] # 初期メンバー
b = ["有安","佐々木","高城","玉井","百田"] # 現在のメンバー
p a & b # 積集合
p a | b # 和集合
p a - b # 差集合（aのみにある： 初期メンバーで、現在のメンバーではない）
p b - a # 差集合（bのみにある： 現在のメンバーで、初期メンバーではない）
|
※Windows環境で実行結果が「["\u9AD8\u57CE",……」のように表示される場合には、ファイルの先頭に#! ruby -Kuを追記すれば正常に文字列が表示されるようになる。
初期のメンバーの名前が含まれる配列aと現在のメンバーの名前が含まれる配列bがあるものとする。積集合と和集合を求める場合は配列a、配列bを前に書いても後に書いても同じ結果になるが、差集合の場合は結果が異なることに注意。
実行結果を見る前に、なつかしのベン図を書いて結果がどうなるかを予想してみよう（図1.1）。
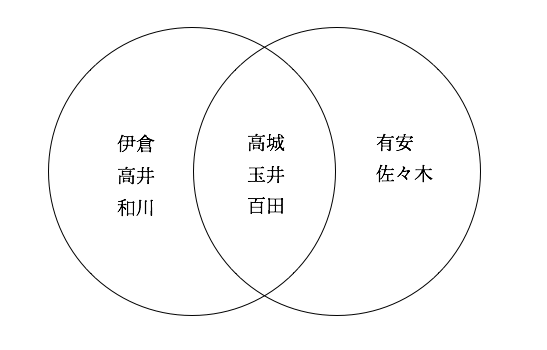
この図を見ると、積集合は["高城", "玉井", "百田"]であるということが予想できる。積集合や差集合についても予想してみよう。
では、実行例を見てみよう。予想通りになっただろうか。
|
$ ruby sample001.rb
["高城", "玉井", "百田"]
["伊倉", "高井", "高城", "玉井", "百田", "和川", "有安", "佐々木"]
["伊倉", "高井", "和川"]
["有安", "佐々木"]
|
積集合と和集合については直感的に結果が分かるが、差集合については演算子の両辺にどちらの配列を書くかによって結果が異なるので注意。a-bならaにあってbにないもの、ということになる。
基本的な集合演算の組み合わせによって、さまざまな集合が求められる。初期メンバーが配列aに、途中のメンバーが配列bに、現在のメンバーが配列cに含まれるとすれば、途中にのみいたメンバーを求めたり、初期メンバーにはいたが、途中で一時離脱して、また復帰したメンバーを求めたりすることもできる。
|
a = ["伊倉","高井","高城","玉井","百田","和川"] # 初期メンバー
b = ["有安","佐々木","高城","玉井","早見","百田"] # 途中のメンバー
c = ["有安","佐々木","高城","玉井","百田"] # 現在のメンバー
p b - a - c # 差集合（bのみにある： 途中にのみいたメンバー）
p a & c - b # 初期メンバーであり、現在のメンバーでもあるが、途中にはいなかった（一時離脱して復帰した）
|
途中にのみいたメンバーは配列bに含まれ、配列aと配列cに含まれない要素なので、b-a-cで求められる。また、一時離脱して復帰したメンバーは、配列aと配列cの両方に含まれ、配列bに含まれない要素なので、a&c-bで求められる。
実行例は以下の通り。
|
$ ruby sample002.rb
["早見"]
[]
|
途中にのみいたメンバーは1人。途中離脱して復帰したメンバーはいないことが分かる。配列a、配列b、配列cの要素をいろいろと変更して、結果がどう変わるか確認してみるといいだろう。
集合の類似度を求める
別の応用例も見てみよう。集合の類似度を表す係数としては、ジャッカード係数、ダイス係数、シンプソン係数などが使われる。これらの係数は以下のようにして求める。
- ジャッカード係数： 積集合の要素数÷和集合の要素数
- ダイス係数： 2×積集合の要素数÷（集合Aの要素数+集合Bの要素数）
- シンプソン係数ｹ： 積集合の要素数÷（集合Aの要素数と集合Bの要素数の小さい方）
この式を見ると、ジャッカード係数は、全体の中でどれぐらい同じものがあるかということを表すことが分かる。一方、シンプソン係数は小さい集合に比べてどれくらい同じものがあるかということを表す。ダイス係数はジャッカード係数とシンプソン係数の間と考えるとよい。これらの係数を求めるメソッドを作ってみよう。
|
def jaccard(a, b)
1.0 * (a&b).length / (a|b).length
end
def dice(a, b)
2.0 * (a&b).length / (a.length + b.length)
end
def simpson(a, b)
1.0 * (a&b).length / [a.length, b.length].min
end
a = ["伊倉","高井","高城","玉井","百田","和川"] # 初期メンバー
b = ["有安","佐々木","高城","玉井","百田"] # 現在のメンバー
puts jaccard(a,b)
puts dice(a,b)
puts simpson(a,b)
|
ジャッカード係数とシンプソン係数を求めるメソッドでも1.0を掛けているのは、整数どうしの割り算になり小数点以下が切り捨てられるのを防ぐためである。メソッドは定義に従って書いただけである。配列（Arrayクラス）のlengthメソッドを使うと配列の要素数が求められる。
実行例も見ておこう。
|
$ ruby sample003.rb
0.375
0.5454545454545454
0.6
|
ダイス係数は、ジャッカード係数とシンプソン係数の間の値になっている。どの係数を使うかは、観点によって決めるとよい。
まとめ
配列の&演算子を利用すれば積集合が求められ、|演算子を利用すれば和集合が求められる。-演算子では差集合が求められるが、-演算子では交換法則が成り立たないことに注意。集合演算はデータベースやWebページの検索などに応用される。
API：Arrayクラス カテゴリ：組み込みライブラリ
API：積集合｜和集合｜差集合｜&演算子｜l演算子｜-演算子 カテゴリ：Arrayクラス
※以下では、本稿の前後を合わせて5回分（第21回～第25回）のみ表示しています。
連載の全タイトルを参照するには、［この記事の連載 INDEX］を参照してください。
21. ファイルから1行／段落ごと読み込む（入力する）には？
Rubyでテキストファイルから文字列を読み込むための方法として、ファイル内の全テキスト内容を先頭から1行単位ずつもしくは1段落ずつループ処理する方法と、ファイルから読み込んだ全ての行を配列として返す方法を説明する。
22. ファイルに文字列を書き込む（出力する）には？
テキストファイルに文字列を書き込むための基本を解説。新規書き込みと追加の方法を確認した後、任意の位置から書き込む方法や読み書き両用モードでファイルを利用する方法を説明する。
23. ファイルの排他制御を行うには？ その際のデッドロック問題とは？
1つのファイルに複数のプログラムから同時アクセスすると、上書きによりデータが消失する可能性がある。これを回避するために排他制御を行う方法と、その際に問題となるデッドロックを回避する方法について説明する。
25. 【現在、表示中】≫ 集合演算を行うには？
Rubyで配列を使って集合演算を行う方法として、「＆」演算子による積集合／「|」演算子による和集合／「-」演算子による差集合を説明する。
