書籍転載：Thinking Machines ― 機械学習とそのハードウェア実装（10）

ディープラーニング（深層学習）の基本：数式モデル

Device & OSS 機械学習ディープラーニング

2017年6月27日

ディープラーニング（深層学習）の一般的なネットワークモデルである「順伝播型ニューラルネットワーク」の、各ユニットにおける演算を表現する数式モデルを示しながら、その意味を説明する。

高野茂幸

　前回は、書籍『Thinking Machines ― 機械学習とそのハードウェア実装』から「第4章機械学習ハードウェア、4.1 実装プラットフォーム」を転載しました。今回は、「付録A 深層学習の基本、A.1 数式モデル」を転載します。

書籍転載について

　本コーナーは、インプレスR＆D［Next Publishing］発行の書籍『Thinking Machines ― 機械学習とそのハードウェア実装』の中から、特にBuild Insiderの読者に有用だと考えられる項目を編集部が選び、同社の許可を得て転載したものです。

　『Thinking Machines ― 機械学習とそのハードウェア実装』（Kindle電子書籍もしくはオンデマンドペーパーバック）の詳細や購入はAmazon.co.jpのページもしくは出版元のページをご覧ください。書籍全体の目次は連載INDEXページに掲載しています。

ご注意

本記事は、書籍の内容を改変することなく、そのまま転載したものです。このため用字用語の統一ルールなどはBuild Insiderのそれとは一致しません。あらかじめご了承ください。

■

付録A　深層学習の基本

　付録Aでは、L層で構成された深層学習の一般的なネットワークモデルである順伝播型ニューラルネットワーク（Feedforward Neural Network）の基本的な事項を紹介する。

　まず各ユニットにおける演算を数式モデル化する。使用しているパラメータ空間図とそれに対応したデータパス図は、実際にハードウェア実装可能なモデルである。

　次に数式モデルを行列演算で表記し、かつ行列演算に使用するデータのレイアウトとそのサイズやパラメータの初期化方法を検討する。

　さらにミニバッチ学習の処理シーケンスを説明する。最後に深層学習モデル開発に伴う課題を取り上げる。

A.1　数式モデル

　ここでは一つのjニューロンの数式モデル表現を検討する。iニューロンがこのjニューロンのシナプスへ接続しているとする。ニューロンはその入力値が活性化関数で表現される、ある条件を満たすと発火して活動電位を出力する。ニューロン間のシナプスにおける接続は、その接続強度を表す重み係数wで表現し、iニューロンの出力値z_iにこの重み係数w_jiを積算した値がjニューロンへの入力になる。jニューロンは先行して接続している全てのiニューロンからの電流を入力し、活性化関数の条件を満たした時に発火して活動電位を出力する。

　順伝播型ニューラルネットワークはこのニューロンの接続を層構造としている。重みとバイアス（後述）を一般にパラメータと呼び、l層でのパラメータの集合（パラメータセット）をl層のパラメータ空間と呼ぶ事にする。また、参考文献【36】では複数の重みとバイアス、活性化関数で構成されるニューロンをユニットと呼んでおり、ここではそれに従っている。

A.1.1　順伝播型ニューラルネットワーク

　任意の(l − 1)層iユニットからl層jユニットへの入力x_i^(l)に対する重みw_ji^(l)による積（w_ji^(l)x_i^(l)）を取る時、このjユニットへの入力の総和u_j^(l)は次のように表される【36】。

u_j^(l) = ∑_iw_ji^(l)x_i^(l) + b_j^(l)

式A.1

　なおb_j^(l)はバイアスである。このjユニットの出力z_j^(l)は活性化関数f_j^(l)(*)へu_j^(l)を入力した結果の出力値であり、

z_j^(l) = f_j^(l)（u_j^(l)）

式A.2

と表される【36】。この出力z_j^(l)は次の層(l + 1)のkユニットの入力x_j^(l + 1)である。活性化関数については後述する。

A.1.2　学習と誤差逆伝播法:パラメータの更新

　任意の(l − 1)層iユニットからの入力要素に対してl層jユニットへの入力の重みw_ji^(l)の更新は次の式で表される【36】。

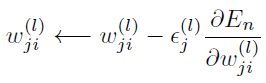
$w^{(l)}_{ji} \longleftarrow w^{(l)}_{ji} - \epsilon^{(l)}_{j}\frac{\partial E_{n}}{\partial w^{(l)}_{ji}} \label{eq:weight_update}$

式A.3

　バイアスも同様の式で表すことができる。ここで、ϵ_j^(l)はl層jユニットの学習係数である。最終層である出力層l = Lでのユニット数をnとする。E_nは誤差関数と呼び、一般にラベルである目標出力（期待値）d_nと実際の最終出力値z_n^(L)の平均二乗誤差であり、最終層Lの誤差はδ^L = E_nと定義する。

　δ^Lを極小値へ収束させ、期待値とできるだけ一致する出力になる様にパラメータの値を調整することが学習である。入力層への入力値全てをまとめて入力ベクトルといい、活性化関数の出力全てをまとめてアクティベーションと呼ぶ。一つのアクティベーションに対して、一つの目標出力値と最終出力値から誤差関数値を得て、これを利用して学習することをオンライン学習と呼ぶ。複数の連続したアクティベーションをまとめてニューラルネットワークへ入力し、複数分の誤差関数値を使用してまとめて学習することをバッチ学習という。まとめている大きさ（バッチサイズという）が大きいと必要なメモリ量が増えるので、適宜バッチサイズを分割して学習する事をミニバッチ学習という。

　このδ^Lの値を用いてパラメータを更新するための値を計算し、出力層（l = L）から入力層（l = 1）の方向へ計算しながら逆伝播させて、パラメータを更新していく。各層での誤差関数のパラメータに関する偏微分は次のように表される【36】。

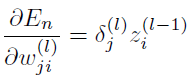
$\frac{\partial E_{n}}{\partial w^{(l)}_{ji}} = \delta_{j}^{(l)}z^{(l-1)}_{i} \label{eq:gradient}$

式A.4

　この時、勾配降下の更新量を決めるδ_j^(l)は次の式から得る【36】。

δ_j^(l) = f ′_j^(l)（u_j^(l)）∑_kw_kj^(l + 1)δ_k^(l + 1)

式A.5

　ここで、f ′_j^(l)(*)はl層jユニットの活性化関数f_j^(l)(*)の一次導関数である。l層においてδ_j^(l)を計算して、この値を隣接する下位層側(入力層側)へ伝播させて勾配を更新するので、この更新方法を誤差逆伝播法と呼ぶ。

A.1.3　活性化関数

　表A.1に深層学習で一般に利用される活性化関数を示す。

活性化関数	f(u)	f ′(u)	Use Case
Hyperbolic Tangent	f(u)=tanh(u)	f ′(u)=1 − tanh²(u)	隠れ層一般
Rectified Linear Unit	f(u)=max(u, 0)	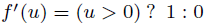$f'(u)= (u > 0)\hspace{2pt}?\hspace{4pt} 1 : 0$	隠れ層一般
Sigmoid	f(u)=1/(1 + e^−u)	f ′（u）=f(u)(1 − f(u))	2値問題の出力層
Softmax	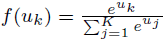$f(u_{k})= \frac{e^{u_{k}}}{\sum_{j=1}^{K}e^{u_{j}}}$	f ′(u_k = f(u_k)−t_k	多クラス問題の出力層

表A.1　Activation Functions【36】.

　Softmaxの一次導関数は後段にCross Entropy（t_kはエントロピー係数とする）があるとした場合のものである。活性化関数f(u)は学習時にその一次導関数を利用するので微分可能である必要があるが、非線形関数であれば良い。

　活性化関数は勾配消失問題を伴う。勾配消失問題とは、例えば活性化関数としてtanh(*)を使うとその関数は上位層（出力側の層）で−1か+1へ飽和しやすく、従って適切に初期化がされないと学習の初期段階で下位層（入力側の層）でf ′(u)はほぼゼロ値になるので勾配の更新量（式A.4）も大抵ゼロ値になる事である【218】。従って下位層で極小値への収束速度が低下する問題であり、さらに良い極小値を得られない時がある。

　Rectified Linear Unit関数（ReLU関数）【219】は入力値がゼロ値より大きい時に活性化（入力値を出力する線形関数の領域の時）し、かつその時のその一次導関数の値は常に“1”である。従って、tanh(*)と異なり上位層で活性化しているユニットはその値を使用したδ_j^(l)が逆伝播するので下位層でも十分な更新量を得られ勾配消失問題は発生しない。とはいえ、ReLU関数は活性化していない時ゼロ値であり勾配もゼロ値になるので学習が低速になる時がある。Leaky ReLU関数（LReLU関数）【218】はこの問題に対応したReLU関数の拡張であり下記のような関数f(u)である。

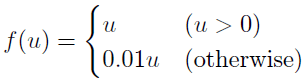
$f(u)= \begin{cases} u & (u > 0)\\ 0.01u & ({\rm otherwise}) \end{cases}$

式A.6

　LReLU関数は活性化していない時も僅かであるが値を出力するので、勾配がゼロ値になる事を防ぐ。さらに入力値u ≤ 0の時の傾き0.01をパラメータ化して一般モデル化したParametric ReLU関数（PReLU関数）がある【220】。2015年時点でPReLU関数を使用してImageNet 2012で高認識率を実現している。

■

　次回は、「付録A 深層学習の基本、A.2 機械学習ハードウェアモデル」を転載します。

【参考文献】

【36】(2)(3)(4)(5)(6)(8) 岡谷貴之. 深層学習. 機械学習プロフェッショナルシリーズ. 講談社, 1st. edition, April 2015.
【218】(2) Andrew L. Maas, Awni Y. Hannun, and Andrew Y. Ng. Rectifier Nonlinearities Improve Neural Network Acoustic Models. In ICML Workshop on Deep Learningfor Audio, Speech, and Language Processing, ICML '13, 2013.
【219】 Xavier Glorot, Antoine Bordes, and Yoshua Bengio. Deep Sparse Rectifier Neural Networks. In Aistats, volume 15, pages 275, 2011.
【220】 Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. CoRR, abs/1502.01852, 2015.

※以下では、本稿の前後を合わせて5回分（第8回～第12回）のみ表示しています。
　連載の全タイトルを参照するには、［この記事の連載 INDEX］を参照してください。

8. ディープラーニングを含むニューラルネットワーク・モデルと、そのハードウェア実装

一般的なニューラルネットワークモデルとディープラーニング（深層学習）について紹介。さらにそのハードウェアを実装するための一般的な方法を説明する。

2017年6月13日(火曜日)

9. 機械学習ハードウェアとは？実装基盤となるメニーコアプロセッサ／DSP／GPU／FPGAのアーキテクチャ概説

機械学習ハードウェアとは、設計開発した機械学習モデルを実行するハードウェアプラットフォームのことだ。その実装プラットフォームとなる「CPUを含むメニーコアプロセッサ」「DSP」「GPU」「FPGA」のアーキテクチャについて概説する。

2017年6月20日(火曜日)

10. 【現在、表示中】≫ ディープラーニング（深層学習）の基本：数式モデル

2017年6月27日(火曜日)

11. 機械学習ハードウェアモデル ― 深層学習の基本

深層学習における、パラメーター空間と順伝播・逆伝播演算の関係を説明。また、代表的な学習の最適化方法と、パラメーターの数値精度についても紹介する。

2017年7月4日(火曜日)

12. 深層学習と行列演算 ― ディープラーニングの基本

「深層学習の行列表現とそのデータサイズ」「行列演算のシーケンス」「パラメーターの初期化」について説明する。

2017年7月11日(火曜日)

書籍転載：Thinking Machines ― 機械学習とそのハードウェア実装（10）