書籍転載：Thinking Machines ― 機械学習とそのハードウェア実装（14）

CNN（畳み込みニューラルネットワーク）／RNN（再帰型ニューラルネットワーク）／AE（自動符号化器）の応用モデル

2017年7月25日

CNN、RNN、AEといったネットワークモデルを拡張あるいは組み合わせた「Deep Convolutional Generative Adversarial Networks」「Highway Networks」「Stacked Denoising Autoencoders」「Ladder Networks」「Residual Networks（ResNet）」を紹介する。

高野茂幸

　前回は、書籍『Thinking Machines ― 機械学習とそのハードウェア実装』から「付録A 深層学習の基本、A.4 ネットワークモデル開発時の課題」を転載しました。今回は、「付録B Advanced Network Models、B.1 CNN Variants、B.2 RNN Variants、B.3 Autoencoder Variants、B.4 Residual Networks」を転載します。

書籍転載について

　本コーナーは、インプレスR＆D［Next Publishing］発行の書籍『Thinking Machines ― 機械学習とそのハードウェア実装』の中から、特にBuild Insiderの読者に有用だと考えられる項目を編集部が選び、同社の許可を得て転載したものです。

　『Thinking Machines ― 機械学習とそのハードウェア実装』（Kindle電子書籍もしくはオンデマンドペーパーバック）の詳細や購入はAmazon.co.jpのページもしくは出版元のページをご覧ください。書籍全体の目次は連載INDEXページに掲載しています。

ご注意

本記事は、書籍の内容を改変することなく、そのまま転載したものです。このため用字用語の統一ルールなどはBuild Insiderのそれとは一致しません。あらかじめご了承ください。

■

付録B　Advanced Network Models

　この章はCNN、RNN、及びAEを応用したネットワークモデルを紹介する。ここで紹介するモデルは前記3つのネットワークモデルの拡張あるいは組み合わせで構成されており、これからのハードウェア開発の際、ネットワークモデルが要求する機能を検討するために用いる事の一助になるだろう。また、より深いネットワークモデルを表現する工夫（ResNet）も説明している。

B.1　CNN Variants

B.1.1　Deep Convolutional Generative Adversarial Networks

　CNNは教師ありモデルとしてよく機能しているが、これに教師なしモデルとして機能するようにGenerative Adversarial Network（GAN）の特性を利用したモデルをDeep Convolutional Generative Adversarial Networks（DCGAN）という【26】。一般に、あるネットワークモデルにおいて入力値から出力値である推論を得るが、DCGANは自動符号化器の復号器のように出力値から入力値を生成する問題を考える。これは前述した訓練データを生成することに相当する。

　GANは生成器（Generator）と分別器（Discriminator）で構成されている。たとえば、生成器が生成する入力値を分別器が真贋として判定する。生成器と分別器がお互いに学習し合って、生成器は入力値同等あるいは一致した値を生成し、分別器はそれが真贋のいずれかを判定する。DCGANは次の様にCNNを変更する事でGANの特性をよく表すモデルを構成する事ができる【26】。

プーリング層は分別器ではストライド有りの畳み込み、生成器は階乗のストライド有りの畳み込みに置き換える。
バッチ正規化を分別器と生成器に使用する。
完全網の隠れ層を削除する。
生成器の出力層以外の層ではReLU関数を使用し、出力層はtanhを使用する。
分別器では全ての層においてLReLU（Leaky ReLU）関数（付録A参照）を使用する。

　パラメータの更新の最適化にはモーメンタムではなく、Adamを用いる。GANの生成器は不安定として知られており、DCGANはこれを補正している。

B.2　RNN Variants

B.2.1　Highway Networks

　Highway Networks【228】はより深いネットワーク構成を組みやすくして、深層でも学習効果を得られ易くしたネットワークモデルである。Highway Networksの各層はベクトルxと重み行列W_Hについてアフィン変換Hを使用して下記のように書ける。

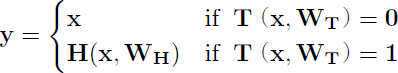
${\bf y} = \begin{cases} {\bf x} & {\rm if}\hspace{5pt} {\bf T}（{\bf x}, {\bf W_{T}}）= {\bf 0}\\ {\bf H}({\bf x}, {\bf W_{H}}) & {\rm if}\hspace{5pt} {\bf T}（{\bf x}, {\bf W_{T}}）= {\bf 1}\\ \end{cases}$

式B.1

　T（x, W_T）= sigmoid（W_T^⊤x + b_T）は変換（Transformation）と呼んでいるアフィン変換である。変換をゼロベクトルあるいは要素全てが1のベクトルと定義する事で、この層の出力を定義している。この時の勾配は次のようになる。

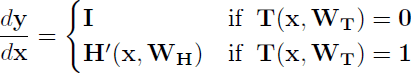
$\frac{{d\bf y}}{{d\bf x}} = \begin{cases} {\bf I} & {\rm if}\hspace{5pt} {\bf T}({\bf x}, {\bf W_{T}}) = {\bf 0}\\ {\bf H'}({\bf x}, {\bf W_{H}}) & {\rm if}\hspace{5pt} {\bf T}({\bf x}, {\bf W_{T}}) = {\bf 1}\\ \end{cases}$

式B.2

　Iは単位ベクトルとする。

B.3　Autoencoder Variants

B.3.1　Stacked Denoising Autoencoders

　Denoising autoencoderは入力データ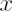 {x} が欠損していても精度の良い出力を可能にするモデルである【229】。入力データ 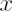{x} からその欠損した入力データ 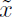$\tilde{x}$ を作り、それをAEの符号噐へ入力して最終的に復号器から入力データ 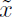$\tilde{x}$ を再構築したzを得る。元の入力データ 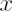{x} とこのzで構築した損失関数において再構築誤差を最小化するように学習することで、欠損した入力データ 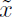$\tilde{x}$ を入力データ 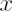{x} に近づかせるパラメータセットを得る。

　Stacked Denoising Autoencoderは、任意のネットワークモデルの学習用データが欠損したデータ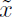 $\tilde{x}$ を多く含む場合にノイズ除去した学習データとして欠損データを含むその学習用データを使用可能にするために提案されたモデルである【229】。l層においてDenoising Autoencoderを使用して得た符号器は、その前の過程（l − 1）で得た層に積層して次のl + 1層の学習に使用される。各ノイズ除去学習で欠損した入力データ 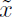$\tilde{x}$ は初回のみに使用する。これにより得た各符号器のパラメータは、次の層への欠損のないデータを生成できる層として使用できる。Denoising Autoencoderによる学習と、それで得た符号器を積層する過程を繰り返して構成したネットワークモデルは、例えばSVMやlogistic regressionといった任意のネットワークモデルのラベル付き学習用データを生成するモデルとして使用できる。

B.3.2　Ladder Networks

　Ladder Networkはもともと教師なし（ラベルなし）学習モデルとして提案されたが【230】、少数のラベル付き訓練データと相対的に多数のラベルなし訓練データで効率よく学習するモデルに拡張されている【231】。あるニューラルネットワークモデル（これをEncoder_clearとする）においてパラメータを更新するためにこのモデルから構築するAEを用意する。AEの符号器はEncoder_clearとパラメータを共有していて、AEとEncoder_clearの相互作用からパラメータを更新する。このL層で構成されたAEのトポロジーはAEの符号器のl層の活性化関数への入力値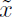 $\tilde{z}^{(l)}$ ^(l)と復号器のL − l層の活性化関数への入力値 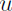${u}$ ^(l + 1)を何らかの組み合わせ関数を利用して組み合わせた値を復号器のL − l層における再構築値 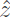$\hat{z}^{(L - l)}$ ^{(L - l)}とし、下位層の詳細表現から離れた上位層を形成する。AEの符号器から 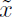$\tilde{z}^{(l)}$ ^(l)を復号器の組み合わせ関数へ入力する経路をラテラル接続と呼ぶ。このAEに壊れた入力値 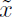$\tilde{x}$ を入力してノイズの入った符号器の出力 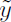$\tilde{y}$ からクロスエントロピー値CEを得る。さらにAEの復号器の再構築値 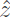$\\hat{z}^{(L - l)}$ ^{(L - l)}と本題のEncoder_clearの活性化関数への入力値z^(l)から層lのコストを得るので、このコストの総和から再構築コストRCを得る。そしてCEとRCの和をコスト関数として学習を行う。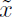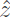 $\tilde{z}^{(l)}$ ^(l)と $\\hat{z}^{(L - l)}$ ^{(L - l)}はそれぞれガウスノイズ付加と正規化をしている。

　訓練データに占めるラベル付き訓練サンプル数の割合が大きいときと小さいとき、組み合わせ関数はそれぞれ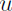 ${u}$ ^{（l + 1）}と 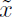$\tilde{z}^{(l)}$ ^(l)の影響を強く受けた値となる【232】。この組み合わせ関数により、ラベル付き訓練サンプル数の割合が大きいとコスト関数はCEの影響を受けたガウスノイズ、割合が小さいときRCの影響を受けたラテラル接続の効果が支配的になり、訓練データに占めるラベル付き訓練サンプル数が変動しても、つまり環境が変化しても対応でき、常に性能を維持できる仕組みになっている。

B.4　Residual Networks

　深層学習においてより深いネットワークモデルの学習は難しい。より深くなると過適応と関係なく精度が飽和するのである。これを論文【233】ではDegradation Problem（劣化問題）と呼んでいる。

　Residual Network（ResNet）は入出力ベクトルを参照する残余関数（Residual Function）を使用してネットワークを再編成したものであり、この方法を使用するとより深いネットワークが構築しやすい【233】。深いネットワークでは勾配消失（付録A参照）しやすく、一般にCNNでは正規化層を挿入する事で対処している。既にある浅いネットワークを使用して深いネットワークを構築するのではなく、前の層の残余（residual）を使用して劣化問題に対応しているのがResidual Networkの特徴である。具体的にはネットワークモデルの層H(x)はF(x):=H(x)−xと残余xの分だけ劣化していると仮定し、これから各層において残余xを付与してH(x):=F(x)+xとすれば、ネットワークモデルを補正できるとしている。ネットワークモデルとしては2つの連続した層の出力にこの2つの層への入力を加算すれば良いと言える。

■

　次回は、「付録C 国別の研究開発動向、C.1 中国、C.2 米国、C.3 欧州、C.4 日本」を転載します。

【参考文献】

【26】(2) Alec Radford, Luke Metz, and Soumith Chintala. Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks. CoRR, abs/1511.06434, 2015.
【228】 Rupesh Kumar Srivastava, Klaus Greff, and Jürgen Schmidhuber. Training Very Deep Networks. CoRR, abs/1507.06228, 2015.
【229】(2) Pascal Vincent, Hugo Larochelle, Isabelle Lajoie, Yoshua Bengio, and Pierre-Antoine Manzagol. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion. J. Mach. Learn. Res., 11:3371-3408, December 2010.
【230】 Harri Valpora. From neural pca to deep unsupervised learning. arXiv preprint arXiv:1441.7783, abs/1511.06430, 2014.
【231】 Antti Rasmus, Harri Valpola, Mikko Honkala, Mathias Berglund, and Tapani Raiko. Semi-Supervised Learning with Ladder Network. CoRR, abs/1507.02672, 2015.
【232】 Mohammad Pezeshki, Linxi Fan, Philemon Brakel, Aaron C. Courville, and Yoshua Bengio. Deconstructing the Ladder Network Architecture. CoRR, abs/1511.06430, 2015.
【233】(2) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep Residual Learning for Image Recognition. CoRR, abs/1512.03385, 2015.

※以下では、本稿の前後を合わせて5回分（第11回～第15回）のみ表示しています。
　連載の全タイトルを参照するには、［この記事の連載 INDEX］を参照してください。

14. 【現在、表示中】≫ CNN（畳み込みニューラルネットワーク）／RNN（再帰型ニューラルネットワーク）／AE（自動符号化器）の応用モデル

2017年7月25日(火曜日)

15. 国別（中国／米国／欧州／日本）の機械学習・AI関連の研究開発動向

機械学習（AIを含む）関連の研究開発を行っている主要な国・地域（中国、米国、ヨーロッパ、日本）における国家水準での取り組みを紹介する。

2017年8月1日(火曜日)

書籍転載：Thinking Machines ― 機械学習とそのハードウェア実装（14）