書籍転載：Thinking Machines ― 機械学習とそのハードウェア実装（7）

機械学習のニューロモルフィック・コンピューティング・モデル

2017年6月9日

機械学習ハードウェアの「ニューロモルフィック・コンピューティング」（前者）と「ニューラル・ネットワーク」という大分類のうち、脳の構造と神経細胞（ニューロン）発火の仕組みを模倣した前者のモデルを説明する。

高野茂幸

　前回は、書籍『Thinking Machines ― 機械学習とそのハードウェア実装』から「第2章従来のアーキテクチャ、2.3 ハードウェア実装のまとめ」を転載しました。今回は、「第3章機械学習と実装方法、3.1 ニューロモルフィックコンピューティング」を転載します。

書籍転載について

　本コーナーは、インプレスR＆D［Next Publishing］発行の書籍『Thinking Machines ― 機械学習とそのハードウェア実装』の中から、特にBuild Insiderの読者に有用だと考えられる項目を編集部が選び、同社の許可を得て転載したものです。

　『Thinking Machines ― 機械学習とそのハードウェア実装』（Kindle電子書籍もしくはオンデマンドペーパーバック）の詳細や購入はAmazon.co.jpのページもしくは出版元のページをご覧ください。書籍全体の目次は連載INDEXページに掲載しています。

ご注意

本記事は、書籍の内容を改変することなく、そのまま転載したものです。このため用字用語の統一ルールなどはBuild Insiderのそれとは一致しません。あらかじめご了承ください。

■

第3章　機械学習と実装方法

　この章では機械学習の基になっている、機械学習ハードウェアの基本構造（アーキテクチャ）を説明する。最初に脳神経網を構成するニューロンについて簡単に説明して、それを利用した2種類の機械学習モデルを紹介する。

　初めに脳の構造とニューロンの発火（後述）の仕組みを模倣したニューロモルフィックコンピューティング（Neuromorphic Computring）モデルを説明する。ニューロモルフィックコンピューティングは発火のタイミングを重要視した仕組みで動作するので、ハードウェアもタイミングをいかに扱うかが重要になっている。ここではニューロンの発火の仕組みを基に本題のハードウェア構成について説明する。また、一般に使用されているAER（Address-Event Representation）というタイミングを取る仕組みも説明する。

　もう一つのモデルであるニューラルネットワークモデルは、一般にディープニューラルネットワーク（Deep Neural Network）や深層学習（Deep Learning）という名でよく知られているモデルを包括している。初めに一般的なニューラルネットワークモデルである、畳み込みニューラルネットワーク（Convolutional Neural Network）、再帰型ニューラルネットワーク（Recurrent Neural Network）、そして自己符号化器（Autoencoder）を紹介して、その後にハードウェア実装について説明する。

　脳の神経細胞（Neuron、ニューロン）の模式図を図3.1(a)に示す。

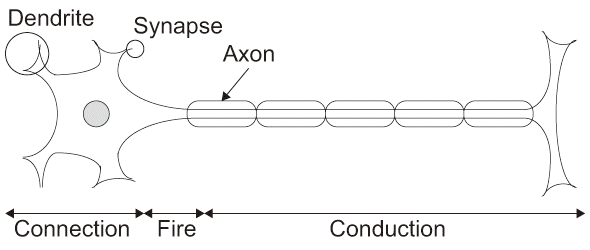
図3.1(a)　Neuron and STDP Model.： Neuron Cell.

　他のニューロンとの接続は樹状突起（Dendrite）先端に複数存在するシナプス（Synapse）で行う。複数のシナプスから来るイオン物質*4の量に応じてニューロン内の電位が上昇し、ある閾値を超えると活動電位（Spikeという）を発生させ（発火するという）、その電位が軸索（Axon）を通り、最終的に接続している他のニューロンに伝達される。

*4　一般的に「神経伝達物質（Neurotransmitter）」と呼ばれる化学伝達物質のことである。本書では論理回路や電子回路との対応を取るため、イオン物質あるいはイオン電流として扱っている。

　このニューロンを形式的に表したのが図3.1(b)である。

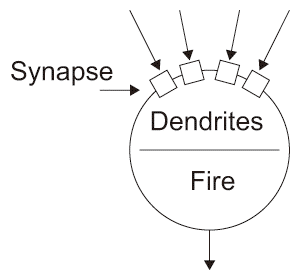
図3.1(b)　Neuron and STDP Model.： Formal Neuron Model.

　シナプスに来る信号に対してシナプスの結合の強さを重み（Weight）係数で表し、重みと入力信号の積の総和が閾値を超えると発火し、何らかの電位を持つ活動電位を出力する。このようなニューロンのモデルを形式ニューロンモデル（Formal Neuron Model【79】）という。従って、ニューロンの集合体である脳はニューロンをノード、Axon以降の部分をエッジとした重み付きグラフで表すことができる。

　機械学習システムには決定木（Decision Tree【80】）や自己組織化マップ（SOM; Self-Organizing Map【81】）等もあるが、現在主要なアプローチはアプリケーションとして応用範囲の広い動物の脳を模倣・応用したシステムである。機械学習ハードウェアの内、脳の構造や機能を模倣したハードウェア実装のアプローチをBrain-inspired Computing（脳創発コンピューティング）という。

　機械学習ハードウェアの大分類として、ニューロモルフィックコンピューティング（Neuromorphic Computing）とニューラルネットワーク（Neural Network）がある。前者は脳のシナプスの機能と発火の仕組みを模倣した実現アプローチで、後者は脳の形式ニューロンモデルの様な機能のみを模倣し統計的手法にも基づいた実現アプローチである。どちらの実現アプローチでも入力信号（入力データ）に対して重みを積算してその総和値からニューロンを発火させる。

3.1　ニューロモルフィックコンピューティング

　ニューロモルフィックコンピューティング（Neuromorphic Computing）はスパイク発火の仕組み等を脳の構造を模倣することでハードウェア実装する実現アプローチであり、Spiking Neural Network（SNN）と呼ぶこともある。

3.1.1　活動電位タイミング依存可塑性と学習

　特定のニューロンにおいて、そのニューロンのシナプスに先行して接続しているニューロンとの結合の強さが特定ニューロンの発火条件と密接に関係があり、ニューロンの学習にも関係しているとみられている。シナプスにおけるその結合の強さ（実効強度）は、その特定ニューロンにおける発火によるスパイクがそのシナプスに到着する時刻と、先行接続しているニューロンにおける発火によるスパイクがそのシナプスに到着する時刻との差により決まるSTDP（Spike Timing Dependent Platicity; 活動電位タイミング依存可塑性【82】）が脳の学習機能を形成しているとみられる。ニューロモルフィックコンピューティングで学習機能を実現する場合、この特性を実装する必要がある。ここではSTDPによる学習の仕組みを説明する（図3.1(c)参照）。

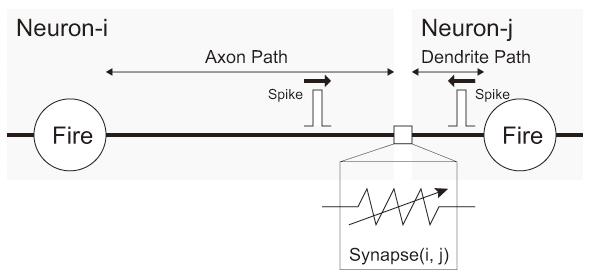
図3.1(c)　Neuron and STDP Model.： STDP Model.

　特定のニューロンの発火に先行接続側のニューロンがスパイクを生成すると、特定のニューロンのシナプスは長期的増進作用（LTP; Long-Term Potentiation）を受け、入力側ニューロンとのシナプス接続の相関が弱くなり実効強度が減少する。また、特定のニューロンの発火に続いて入力側のニューロンがスパイクを生成すると、特定のニューロンのシナプスは長期的減退作用（LTD; Long-Term Depression）を受け、入力側ニューロンとのシナプス接続の相関が強くなり実効強度が増加する。LTPとLTDはその時間差の大きさが小さいほど指数的に大きい特性を持つ。

　発火による実効強度の変化は、特定ニューロンでの発火とそのニューロンに先行して接続しているニューロンにおける発火の時間間隔が短いほど大きな変化がある関数として数式モデル化できる。つまり、シナプスの実効強度をスパイク生成の時間間隔の指数的減少関数として数式モデル化する。先行するニューロンでの発火に続いてそれに接続している特定のニューロンで発火する時、この時間差分は正の値でありLTPである。また、特定のニューロンでの発火に続いて先行するニューロンで発火する時、時間差分は負の値でありLTDである。LTPとLTDどちらも時間間隔が大きい時、伝導性の変化は小さく、時間間隔が小さい場合その変化は指数的に大きい。

　以上を踏まえて論文【83】から次のように活動電位を数式モデル化できる。ここでニューロンの発火の時間差情報や発火時刻をニューロン間で共有せず、電位の伝播の相互作用により発火し、かつ各シナプスの結合強度に影響を与えると仮定する。特定ニューロンjの時刻tにおける電位をV_neuron^(j)(t)、先行接続しているニューロンiの時刻tにおける電位をV_neuron⁽ⁱ⁾(t)、特定ニューロンjと先行ニューロンiの間のシナプスに到着するそれぞれのニューロンからの電位をV_neuron^(j)（t + δ_i^(j)）とV_neuron⁽ⁱ⁾（t + δ_j⁽ⁱ⁾）とする。δ_i^(j)とδ_j⁽ⁱ⁾はそれぞれのニューロンから、その特定シナプスまで到着するのに要する遅延時間である。特定ニューロンjの発火条件を定義する活性化関数をf^(j)(*)、そのシナプスの実効強度を時刻tにおいてw_i^(j)（t）とすると、ニューロンjへ流入するイオン物質の総量I^(j)(t)は以下の様になる。

I^(j)（t）=∑_iw_i^(j)（t − δ_i^(j)）V_neuron⁽ⁱ⁾（t − δ_i^(j) − δ_j⁽ⁱ⁾）

式3.1

　このイオン物質の総量I^(j)（t）により、ニューロンの発火条件を定義している活性化関数f^(j)(*)による時刻tにおけるニューロンjの電位V_neuron^(j)（t）は次の様に書ける。

V_neuron^(j)(t)=f^(j)(I^(j)(t))

式3.2

　V_neuron^(j)(t)≫0の時、ニューロンjは時刻tで発火して活動電位を生成した事に相当する。シナプスにおける実効強度w_i^(j)(t)は学習係数1 > ϵ > 0と実効強度の更新量である電導率の変化量S_i^(j)(t)を使用して以下の様になる。

w_i^(j)（t + δ_t）=w_i^(j)(t)−ϵS_i^(j)(t)

式3.3

　δ_t > 0は考慮可能な時間の最小単位とする。以上のことから脳の学習はニューロンのシナプスの実効強度、つまり電導率であるwを更新することに相当する。

3.1.2　ニューロモルフィックコンピューティングハードウェア

　ニューロモルフィックコンピューティングのハードウェア構成を図3.2(a)に示す。

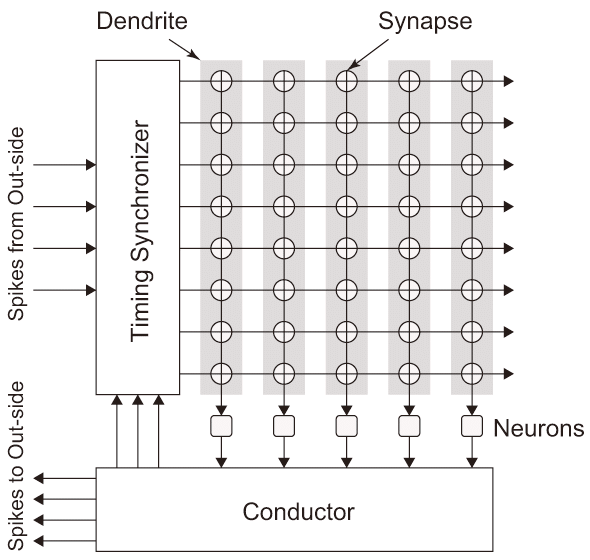
図3.2(a)　Neuron and STDP Model.： Neuromorphic Computing Hardware Basic Structure.

　一般にニューロモルフィックコンピューティング・アーキテクチャは活動電位を単位の大きさとした、ある時刻に発火したパルス波としてSTDPを模倣している。ニューロンは複数のシナプスで構成されたDendrite部と発火を行うNeuron部で構成され（この構成を一般にSomaという）、複数のSomaをクラスタ化し（図3.2(a)では5つの列としてクラスタ実装している）、入力したスパイクを各Somaで共有する構成を取って複雑なグラフを構築できるようにしている。

　入力スパイクはSomaへの入力タイミングがTiming Synchronizerで調整された後、複数のシナプスで構成されたアレイに送信される。各ニューロンはDendriteからの出力値を入力して何らかの条件を満たした時にスパイクを発火させる。発火したスパイクはConductorで収集され、出力できるデータフォーマットに整えた後に出力、あるいは自分のこのユニットにフィードバックする。このユニットをコア・モジュールとしてチップ上に複数個これを並べて実装して全体的な脳を構成する。

　このモデルの小分類としてその実装方法から二つに分類できる。入力スパイクとSoma内のシナプスの電導率wの積、そのSomaにおける積算値の総和の仕方（つまり内積演算の仕方）が従来のデジタル回路実装に基づいたモデル（Digital Logic Circuit）と、アナログ回路実装に基づいたモデル（Analog Logic Circuit）である。

デジタル回路（Digital Logic Circuit）
Dendrite内の各シナプスはクロスバー・スイッチで実装され、図3.2(a)のDendriteアレイは全体としてクロスバー・スイッチアレイを構成する。任意の時刻に一つの入力スパイクをTiming Synchronizerから特定のクロスバーの行へ入力し、シナプスであるスイッチが“ON”の時にそのクロスポイントをスパイクが通過してニューロンへ入力される。
複数のDendriteはその入力スパイクを共有しているので、各Dendriteにおいてそのスパイクは適宜クロスポイントを通り特定の一つ以上のニューロンへ入力される。各Dendriteにおいて一つの入力スパイクのみクロスバーに入力されるので、特定のニューロンが先行接続しているN個のニューロンと接続している場合、N個のスパイクをクロスバーに入力させてニューロンはDendriteからの入力値を累算（Accumulation）する必要があるので、ニューロンへ流入するイオン物質の総量Iを得るまでNステップを要する。
また、活動電位の生成はイオン物質の総量Iに基づいて発火するように論理演算回路で実装されている。シナプスがクロススイッチで構成されているので、シナプスの伝導率はスパイク同様に単位値であり実効強度を表していないので、それに合わせてNeuronの発火条件を調整する仕組みが必要である。さらにクロックを利用する（同期回路）アーキテクチャと利用しない（非同期回路）アーキテクチャに分類できる。
アナログ回路（Analog Logic Circuit）
内積演算がアナログ回路で実装されている。Dendriteのシナプスは実効強度wを記憶する記憶素子で実装され、図3.2(a)の Dendriteアレイは全体としてメモリセル・アレイ相当になる。Timing Synchronizerからの出力線がメモリセル・アレイのアドレス線に相当する。任意の時刻に一つ以上の入力スパイクをTiming Synchronizerからメモリセル・アレイの各アドレス線へ出力して各Dendriteでメモリ値の読み出しの要領で値を読み出す。各記憶素子（シナプス）において、入力スパイクの電位とシナプスの電導率の積からそのシナプスにおける電流をデータの読み出しラインへ出力する。一つ以上のスパイクと実効強度の積算値が電流として各Dendriteへ流入するので、一つのDendrite上で複数の読み出しが発生して複数の電流が合流することからDendriteはアナログ加算器、そしてシナプスに相当するメモリセルはアナログ積算器とみなす事ができ、一つのDendriteは一つのアナログ内積演算回路に相当する。メモリセルとして、PCM、ReRAM、そしてSTT-RAM等の記憶素子を利用している。

3.1.3　AER：Address-Event Representation

　アナログ回路実装、デジタル回路実装ともに実装したニューロンの集合をクラスタ化してコアとして扱っている。

　ニューロモルフィックコンピューティングではニューロンの間でのスパイク情報の通信にAER（Address-Event Representation【75】）を使用しているので、このAERについて説明する。

　一般にAERはニューロンの集合体であるコア内の各ニューロンに付与してあるID番号列で構成されている。発火したスパイクを順にニューロンのIDで表記してこれを接続先のニューロンへ送信するのである。つまり時間共有（time-multiplexing）でスパイクを送信する。

　送信先のニューロンは別のコアや別のチップにある可能性がある。従って一般にその送信元のコアのアドレス、チップのアドレス、そしてニューロンIDから送信先ニューロンのコアのアドレスとチップのアドレス、およびニューロンIDを入手する仕組みが必要である。複数のニューロンが同時に発火することも起こり得るのでそのための調停回路を設ける場合がある。調停回路を設けずにCollisionとして扱う場合もある。そして、FIFOを実装して送信待ち用のバッファを実装する。

　Δ/n秒毎のAddress変換、転送、そして逆変換のタイミングが必要になる【84】。ここでΔは発火の時間間隔、nは同時に発火する最大ニューロン数である。

■

　次回は、「第3章機械学習と実装方法、3.2 ニューラルネットワーク」を転載します。

【参考文献】

【75】 Mask-Programmable Logic Devices, June 1996.
【79】 Warren S. McCulloch and Walter Pitts. Neurocomputing: Foundations of Research, chapter A Logical Calculus of the Ideas Immanent in Nervous Activity, pages 15-27. MIT Press, Cambridge, MA, USA, 1988.
【80】 J. R. Quinlan. Simplifying Decision Trees. Int. J. Man-Mach. Stud., 27(3):221-234, September 1987.
【81】 Teuvo Kohonen. 自己組織化マップ. シュプリンガーフェアラーク東京. June 2005.
【82】 Henry Markram, Joachim Lübke, Michael Frotscher, and Bert Sakmann. Regulation of Synaptic Efficacy by Coincidence of Postsynaptic APs and EPSPs. Science, 275(5297):213-215, 1997.
【83】 G. S. Snider. Spike-timing-dependent learning in memristive nanodevices. In 2008 IEEE International Symposium on Nanoscale Architectures, pages 85-92, June 2008.
【84】 K. A. Boahen. Point-to-point connectivity between neuromorphic chips using address events. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 47(5):416-434, May 2000.

※以下では、本稿の前後を合わせて5回分（第5回～第9回）のみ表示しています。
　連載の全タイトルを参照するには、［この記事の連載 INDEX］を参照してください。

5. 機械学習ハードウェアの基礎知識：特定用途向け集積回路「ASIC」

特定アプリケーションに特化した回路を集積する方法であるASICについて概説。アプリケーションを表現するアルゴリズムのソフトウェア実装とASIC実装を比較しながらASIC実装の特徴と制約を説明する。

2017年5月23日(火曜日)

6. 機械学習のハードウェア化の歴史と、深層学習の登場

1980年代～現在まで、機械学習のハードウェア実装の歴史を振り返る。計算機アーキテクチャの行き詰まりと深層学習の登場により、機械学習ハードウェアの研究が進んできたことを紹介する。

2017年5月30日(火曜日)

7. 【現在、表示中】≫ 機械学習のニューロモルフィック・コンピューティング・モデル

2017年6月9日(金曜日)

8. ディープラーニングを含むニューラルネットワーク・モデルと、そのハードウェア実装

一般的なニューラルネットワークモデルとディープラーニング（深層学習）について紹介。さらにそのハードウェアを実装するための一般的な方法を説明する。

2017年6月13日(火曜日)

9. 機械学習ハードウェアとは？実装基盤となるメニーコアプロセッサ／DSP／GPU／FPGAのアーキテクチャ概説

機械学習ハードウェアとは、設計開発した機械学習モデルを実行するハードウェアプラットフォームのことだ。その実装プラットフォームとなる「CPUを含むメニーコアプロセッサ」「DSP」「GPU」「FPGA」のアーキテクチャについて概説する。

2017年6月20日(火曜日)

書籍転載：Thinking Machines ― 機械学習とそのハードウェア実装（7）